Implementing MBR in Swift
In a recent use case, I have implemented an original use case that leverages the power of iOS ARKit. In this use case, we use the iPhone to find the 3d box that will best fit a cloud of 3D points. The idea is to minimize the 3D volume. This article will focus on the first part, where we implement the algorithm that compute the 2D MBR (Miminum Boxing Rectangle). In the following picture the representation of the 2D MBR is the green rectangle.
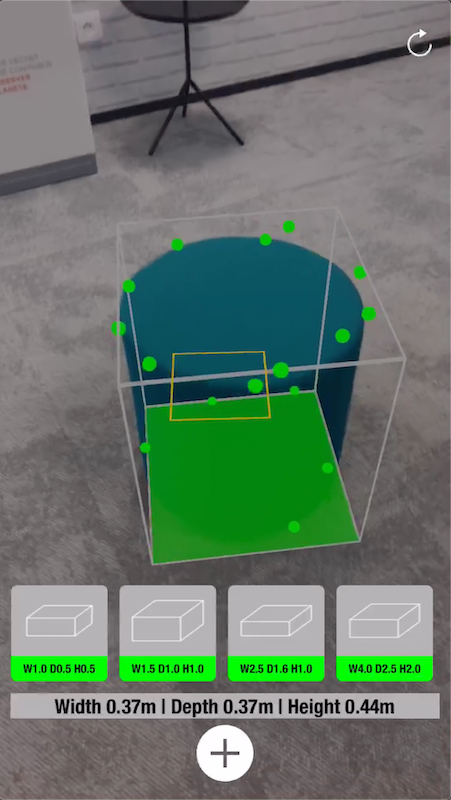
The final 3D MBR that fits the green dot cloud points.
1- Minimal Convex Hull
This is a common problem that is studied since the 70’s. I implement the Andrew’s monotone chain convex hull algorithm to compute the minimal convex hull in 2 dimensions. The algorithm complexity is O(n log(n)). This will easily cover our use case. In this algorithm:
- First, the point cloud is sorted lexicographically.
- Secondly, we enumerate each point to build the upper convex hull.
- Thirdly, we enumerate each point to build the lower convex hull.
- We append the lower convex hull to the upper.
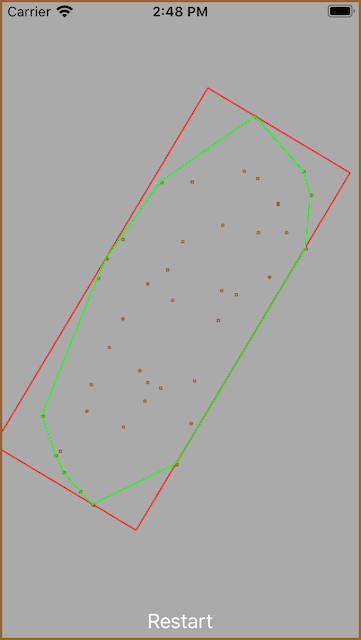
Brown dot->point cloud ; Green->convex hull ; Red -> MBR
2- Rotating calipers
To find the rectangle that will minimize the area, we use the Rotating Calipers algorithm. The complexity is linear in O(n). The idea of the Rotating Calipers, is to rotate the bounding box by each edge of the convex hull. For each orientation we compute the area and we keep the orientation that gives the minimal area.
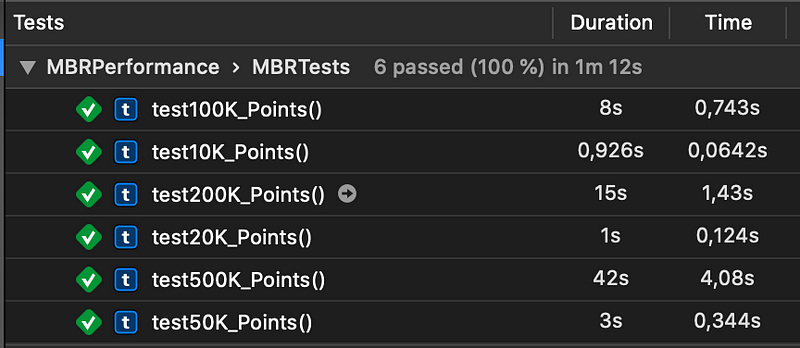
3- Performances
Here are some performance test for the 2D MBR algorithm. These tests have been measured on an iPhone X. We can observe that we compute the 2D MBR with 500K points in a reasonable time (Mean is 4,08 seconds).